Getting Started with Nonconsecutive Sudoku
Getting Started with Nonconsecutive Sudoku
This tutorial applies to:
- https://www.bookpublishertools.com/product/puzzle-maker-pro-nonconsecutive-sudoku-9x9
- Puzzle Maker Pro - Nonconsecutive Sudoku Other Squares
Nonconsecutive Sudoku
Nonconsecutive Sudoku is a sudouk variation with additional rules for the grid: consecutive numbers cannot be adjacent. In other words, when there's a 3 in a cell, the cells next to it - horizontally and vertically - cannot contain a 2 or a 4.
In our modules for Nonconsecutive Sudoku, the highest and lowest numbers are considered consecutive as well: In a 9x9 grid, the 1 and 9 can also not be adjacent to each other.
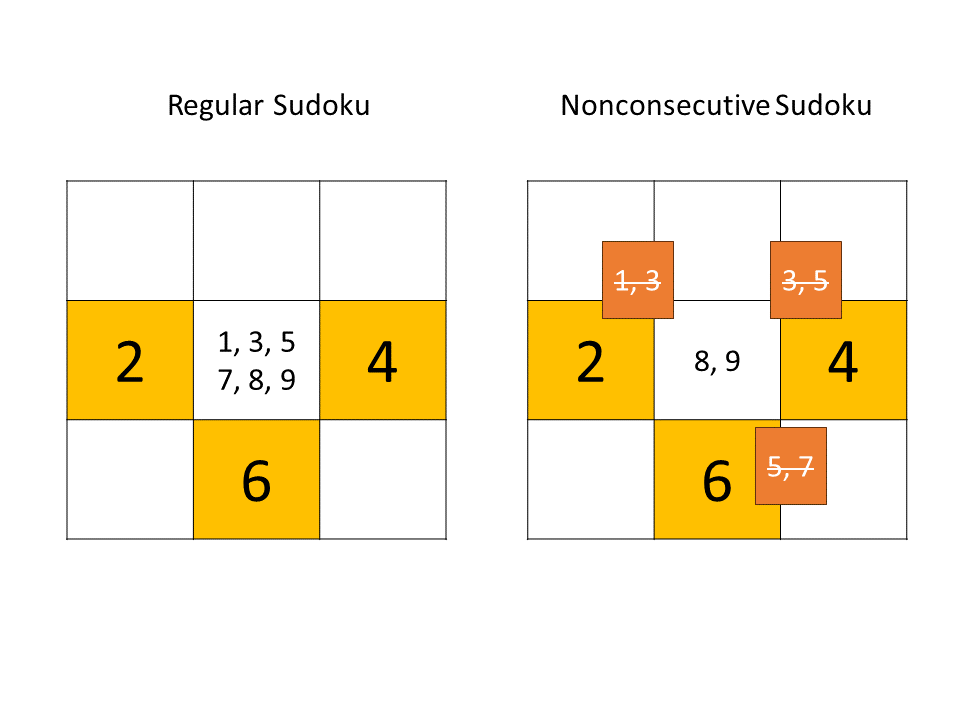
This image illustrates the impact of this rule: In a regular sudoku, if the numbers 2, 4 and 6 would be placed like this, there would be 6 available numbers for the center cell: 1, 3, 5, 7, 8 and 9. (in a 9x9 grid sudoku).
For Nonconsecutive Sudoku there are quite a few restrictions:
- the 2 removes the 1 and 3 from the options
- the 4 removes the 3 and 5 from the options
- the 6 removes the 5 and 7 from the options
Instead of 6 different numbers, there are only 2 options for the center cell: the 8 and 9. The cell at the bottom left also borders to the 2 and 6, therefor removing the 1, 3, 5 and 7 from the options. This cell can only contain the 8 and 9 as well. If one of these two cells contains the 8, the other must have the 9 - only 2 different options. Compared to 6 * 5 = 30 options for regular sudoku.
As you can see the nonconsecutive rule hugely diminishes the number of options for the grids. As a result, there are significantly fewer nonconsecutive sudoku puzzles available.
Find Nonconsecutive Sudoku in Puzzle Maker Pro
To create Nonconsecutive Sudoku puzzles in Puzzle Maker Pro:

- Go to Sudoku Variations
- Select one of the Sudoku Grid Sizes that are available for Nonconsecutive Sudoku (6x6, 8x8, 9x9, 10x10, 12x12, 14x14, 15x15, 16x16)
- Select "Nonconsecutive" in the Variation menu.
There are quite a few tutorials about all the regular features of Sudoku in Puzzle Maker Pro, ranging from grid setup to symbol options, please check the tutorials below.
Note: Even though it's possible to use images for Nonconsecutive Sudokus, it doesn't make much sense, and the sudokus may be impossible to solve, since there are no odd and even images.